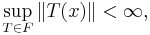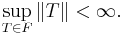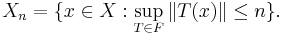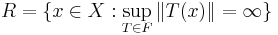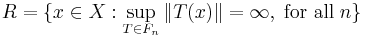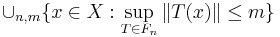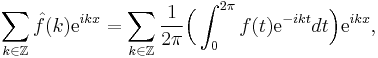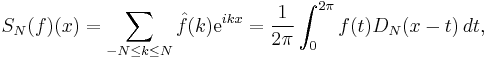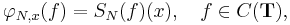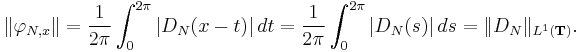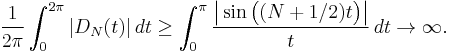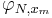Uniform boundedness principle

In mathematics, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis. Together with the Hahn–Banach theorem and the open mapping theorem, it is considered one of the cornerstones of the field. In its basic form, it asserts that for a family of continuous linear operators (and thus bounded operators) whose domain is a Banach space, pointwise boundedness is equivalent to uniform boundedness in operator norm.

The theorem was first published in 1927 by Stefan Banach and Hugo Steinhaus but it was also proven independently by Hans Hahn.

1 Uniform boundedness principle
- 1.1 An example: pointwise convergence of Fourier series
2 Generalizations
3 See also
4 References

Uniform boundedness principle

The precise statement of the result is:

Theorem. Let X be a Banach space and Y be a normed vector space. Suppose that F is a collection of continuous linear operators from X to Y. The uniform boundedness principle states that if for all x in X we have

$\sup_{T \in F} \|T (x)\| < \infty,$

then

$\sup_{T \in F} \|T\| < \infty.$

The completeness of X enables the following short proof, using the Baire category theorem:

Proof.

Define the closed sets X_n with n = 1, 2, 3, … by

$X_n = \{ x \in X�: \sup_{T \in F} \|T(x)\| \le n \}.$

By hypothesis, the union of all the X_n is X. Since X is a Baire space, one of the X_n, say X_m, has an interior point (X_n are closed sets), i.e., there exists a δ > 0 and a y in X such that all x ∈ X with ||x − y|| < δ are elements of X_m. Now, choose an arbitrary z in X with ||z|| < δ. Then, y and y + z are elements of X_m and hence, for every operator T in the family F, ||T(z)|| ≤ ||T(y + z)|| + ||T(y)|| ≤ m + m = 2m. Since z is arbitrary in the ball of radius δ, it follows that ||T|| ≤ 2m / δ for all T in F, which proves the theorem.

A direct consequence is:

Corollary. If a sequence of bounded operators (T_n) converges pointwise, that is, lim T_n(x) exists for all x in X, then these pointwise limits define a bounded operator T.

Note it is not claimed above that T_n converges to T in operator norm, i.e. uniformly on bounded sets. (However, since {T_n} is bounded in operator norm, and the limit operator T is continuous, a standard "3-ε" estimate shows that T_n converges to T uniformly on compact sets.)

Another corollary is that any weakly bounded subset S in a normed space Y is bounded; indeed, the elements of S define a pointwise bounded family of continuous linear forms on the Banach space X = Y^∗, continuous dual of Y. By the uniform boundedness principle, the norms of elements of S, as functionals on X, that is, norms in the second dual Y^∗∗, are bounded. But for every s ∈ S, the norm in the second dual coincides with the norm in Y, by a consequence of the Hahn–Banach theorem.

Let L(X, Y) denote the continuous operators from X to Y, with the operator norm. If the collection F is unbounded in L(X, Y), then by the uniform boundedness principle, the set

$R = \{ x \in X�: \sup_{T \in F} \|T(x)\| = \infty \}$

is not empty. In fact, it is dense in X. The complement of R in X is the countable union of closed sets ∪X_n. By the argument used in proving the theorem, each X_n is nowhere dense, i.e. the subset ∪X_n is of first category. Therefore R is the complement of a subset of first category in a Baire space. By definition of a Baire space, such sets (called residual sets) are dense. Such reasoning leads to the principle of condensation of singularities, which can be formulated as follows:

Theorem. Let X be a Banach space, {Y_n} a sequence of normed vector spaces, and F_n a unbounded family in L(X, Y_n). Then the set

$R = \{ x \in X�: \sup_{T \in F_n} \|T (x)\| = \infty, \; \mbox{for all} \; n \}$

is dense in X.

Proof.

The complement of R is the countable union

$\cup_{n,m} \{ x \in X�: \sup_{T \in F_n} \|T(x)\| \le m \}$

of sets of first category. Therefore its residual set R is dense.

An example: pointwise convergence of Fourier series

Let T be the circle, and let C(T) be the Banach space of continuous functions on T, with the uniform norm. Using the uniform boundedness principle, one can show that the Fourier series, "typically", does not converge pointwise for elements in C(T).

For ƒ in C(T), its Fourier series is defined by

$\sum_{k \in \mathbb{Z}} \hat{f}(k) \mathrm{e}^{ikx} = \sum_{k \in \mathbb{Z}}\frac{1}{2 \pi} \Bigl( \int_0 ^{2 \pi} f(t) \mathrm{e}^{-ikt} dt \Bigr) \mathrm{e}^{ikx},$

and the N-th symmetric partial sum is

$S_N(f)(x) = \sum_{ -N \leq k \leq N } \hat{f}(k) \mathrm{e}^{ikx} = \frac{1}{2 \pi} \int_0 ^{2 \pi} f(t) D_N(x - t) \, dt,$

where D_N is the N-th Dirichlet kernel. Fix x in T and consider the convergence of {S_N(ƒ)(x)}. The functional φ_{N, x} : C(T) → C defined by

$\varphi_{N, x} (f) = S_N(f)(x), \quad f \in C(\mathbf{T}),$

is bounded. The norm of φ_{N, x}, in the dual of C(T), is the norm of the signed measure (2π)⁻¹D_N(x−t) dt, namely

$\| \varphi_{N, x} \| = \frac{1}{2 \pi} \int_0 ^{2 \pi} | D_N(x-t) | \, dt = \frac{1}{2 \pi} \int_0 ^{2 \pi} | D_N(s) | \, ds = \| D_N \|_{L^1(\mathbf{T})}.$

One can verify that

$\frac{1}{2 \pi} \int_0 ^{2 \pi} | D_N(t) | \, dt \ge \int_0^\pi \frac{\bigl|\sin\bigl( (N%2B1/2)t \bigr)\bigr|} t \, dt \rightarrow \infty.$

So the collection {φ_{N, x}} is unbounded in C(T)^∗, the dual of C(T). Therefore by the uniform boundedness principle, for any x in T, the set of continuous functions whose Fourier series diverges at x is dense in C(T).

More can be concluded by applying the principle of condensation of singularities. Let {x_m} be a dense sequence in T. Define

$\varphi_{N, x_m}$

in the similar way as above. The principle of condensation of singularities then says that the set of continuous functions whose Fourier series diverges at each x_m is dense in C(T) (however, the Fourier series of a continuous function ƒ converges to ƒ(x) for almost every x ∈ T, by Carleson's theorem).

Generalizations

The least restrictive setting for the uniform boundedness principle is a barrelled space where the following generalized version of the theorem holds (Bourbaki 1987, Theorem III.2.1):

Given a barrelled space X and a locally convex space Y, then any family of pointwise bounded continuous linear mappings from X to Y is equicontinuous (even uniformly equicontinuous).

Alternatively, the statement also holds whenever X is a Baire space and Y is a locally convex space (Shtern 2001).

Dieudonné (1970) proves a weaker form of this theorem with Fréchet spaces rather than the usual Banach spaces. Specifically,

Let X be a Fréchet space, Y a normed space, and H a set of continuous linear mappings of X into Y. If 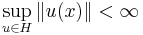$\sup_{u\in H}\|u(x)\|<\infty$ for every x∈X, then the family H is equicontinuous.

References

Banach, Stefan; Steinhaus, Hugo (1927), "Sur le principe de la condensation de singularités", Fundamenta Mathematicae 9: 50–61, http://matwbn.icm.edu.pl/ksiazki/fm/fm9/fm918.pdf . (French)
Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Springer, ISBN 978-3540423386
Dieudonné, Jean (1970), Treatise on analysis, Volume 2, Academic Press .
Rudin, Walter (1966), Real and complex analysis, McGraw-Hill .
Shtern, A.I. (2001), "Uniform boundedness principle", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=b/b015200 .

Uniform boundedness principle

Contents